1.3 Nichtdeterministischer EA (NEA)
Bis anhin haben wir deterministische endliche Automaten (DEA) kennengelernt. Für jede Eingabe bei jedem Zustand war also klar, welcher Zustand der nächste ist.
Nun lassen wir zu, dass diese Übergänge nicht mehr eindeutig sind. Diese endliche Automaten heissen nichtdeterministische endliche Automaten (NEA). Beim Entwerfen eines EA ist es vielmals einfacher, einen NEA anstelle eines DEA zu konstruieren.
Beispiel NEA
Beim folgenden NEA ist nicht eindeutig, welcher Zustand nach \(q_0\) folgt, wenn die nächste Eingabe \(0\) ist. Sowohl \(q_0\) als auch \(q_1\) können Folgezustände sein. In der Übergangstabelle notieren wir in einem solchen Fall die Menge, welche alle Möglichkeiten beinhaltet. Hier betrifft dies \(δ(q_0, 0) = \{q_0, q_1\}\). Weiter sieht man in diesem Beispiel, dass von \(q_1\) ausgehend kein Pfeil mit \(0\) beschriftet ist. Es gibt also keinen Folgezustand von \(q_1\) für die Eingabe \(0\). Danach ist es egal, ob noch weitere Eingaben folgen. Wir landen somit in einer Sackgasse. Der Automat bricht ab und wir landen in keinem Zustand. In der Übergangstabelle schreiben wir in diesem Fall das Symbol \( \emptyset \), das Zeichen für die leere Menge.
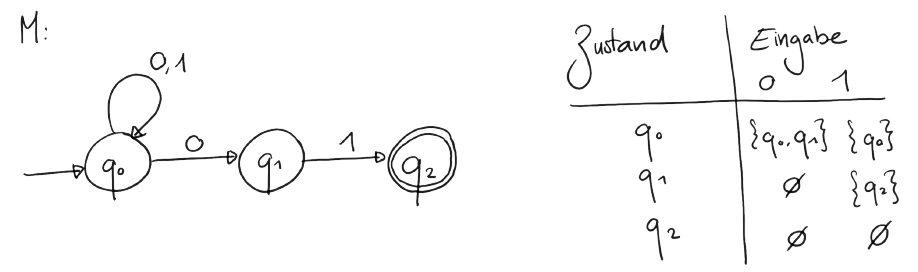
Definition: nichtdeterministischer endlicher Automat (NEA)
Ein nichtdeterministischer endlicher Automat (NEA) ist ein 5-Tupel \(M = (Q, Σ, \delta, q_0, F)\) wobei \( Q, Σ, q_0\) und \( F\) wie beim DEA definiert sind und die Übergangsfunktion \(δ \) definiert ist als
\(δ : Q×Σ → P(Q)\).
Übungen
- In welchem Zustand landet der NEA \(M\) (siehe Beispiel oben) für das Wort 1001?
Wir könnten im akzeptierenden Zustand \(q_2\) landen. Wir könnten aber auch in \(q_0\) oder in einer Sackgasse (also in keinem Zustand) landen. - In welchem Zustand landet der NEA \(M\) für das Wort 1010?
Wir könnten im Zustand \(q_0\), im Zustand \(q_1\) oder in einer Sackgasse landen. Mit dem Wort 1010 landen wir in keinem Fall im akzeptierenden Zustand \(q_2\). - Wichtig wird später sein, ob wir in einem akzeptierenden Zustand landen können.
Welche Wörter können beim NEA \(M\) in einem akzeptierenden Zustand landen? Lösung
Äquivalenz von DEA und NEA
Ein DEA ist ein Spezialfall eines NEA. (Die Übergänge eines NEA’s, müssen nicht eindeutig sein, dürfen dies aber.) Etwas überraschender ist, dass man jeden NEA in einen DEA umwandeln kann. Dies geschieht mittels einer geschickten Teilmengenkonstruktion.
Beispiel NEA zu DEA
Der zu \(M\) (derselbe NEA vom Beispiel oben) äquivalente DEA sieht folgendermassen aus.
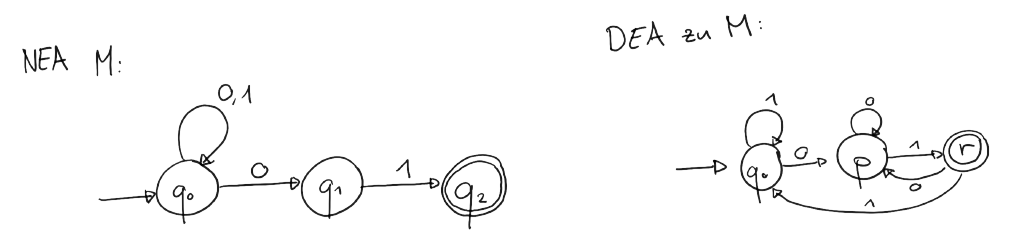
Wie diese Umwandlung genauer passiert, können Sie im folgenden Video sehen und hören. Wir werden die Teilmengenkonstruktion hier nicht weiter behandeln. Wichtig ist zu verstehen, dass man jeden NEA zu einem DEA (und umgekehrt) umwandeln kann.
Hier haben Sie die Option Ihre Notizen zu diesem Abschnitt hochzuladen. Wir empfehlen eine sinnvolle Beschriftung z.B. 1_3_NEA_Notizen.