3.2 Akzeptierender Mechanismus: Automaten
Als akzeptierende Mechanismen lösen Automaten Entscheidungsprobleme.
Landet ein Automat \(M\) für ein Wort \(x\) in einem akzeptierenden Zustand, so sagt man “\(M\) akzeptiert das Wort \(x\)“, “\(x\) ist in der Sprache \(L(M)\)” oder mathematisch “\(x \in L(M)\)“.
Definition: Sprache eines Automaten
Die Sprache \(L(M)\) eines endlichen Automaten \(M\) ist die Menge aller von \(M\) akzeptierten Wörter:
Für deterministische EA \(M\) gilt:
\(L(M) = \{w \in Σ^∗ | \) \(M\) landet für \(w\) in einem akzeptierenden Zustand\(\}\)
Für nichtdeterministische EA \(M\) gilt:
\(L(M) = \{w \in Σ^∗ | \) \(M\) kann für \(w\) in einem akzeptierenden Zustand landen\(\}\)
Bemerkungen
- Jeder Automat akzeptiert genau eine Sprache.
- Umgekehrt aber kann man für eine Sprache verschiedene Automaten bauen. Automaten, die dieselbe Sprache akzeptieren, heissen äquivalent.
- Die Äquivalenz der endlichen Automaten DEA, NEA und ε-NEA führt uns zu den folgenden Äquivalenzen:
Es gibt einen DEA, der die Sprache L akzeptiert. ⇔ Es gibt einen NEA, der die Sprache L akzeptiert. ⇔Es gibt einen ε-NEA, der die Sprache \(L\) akzeptiert.
Kellerautomaten (wie auch die kurz erwähnten Turingmaschinen) lassen sich im Allgemeinen nicht in einen endlichen Automaten umwandeln. So ist es sinnvoll, Klassen von Sprachen zu bilden, die davon abhängen, welche Art von Automat sie akzeptiert. Da endliche Automaten zu regulären Ausdrücken äquivalent sind, akzeptieren bzw. beschreiben sie dieselbe Sprachklasse.
Definition: Klasse der regulären Sprachen
Die Klasse der regulären Sprachen (RS) beinhaltet alle Sprachen, die von einem endlichen Automaten akzeptiert (oder von einem regulären Ausdruck beschrieben) werden.
Jede dieser Sprachen wird regulär genannt.
Es gibt äquivalente Definitionen. Eine ist beispielsweise in Abschnitt 3.3 zu finden und verwendet reguläre Ausdrücke.
Speziell im Sinne von endlichen Automaten halten wir etwas formaler fest:
Definition: regulär
Eine Sprache \(A\) über dem Alphabet \(Σ\) heisst regulär, falls \(A = L(M)\) für einen endlichen Automaten \(M\) gilt.
Beispiel
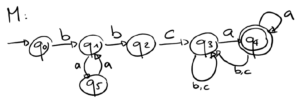
Die Sprache vom DEA \(M\) ist die reguläre Sprache \(L(M) = \{ bxbcya | x = a^n \) für \(n\) gerade & \( y \in \{a, b, c\}^*\}\).
Definition: Klasse der kontextfreien Sprachen
Die Klasse der kontextfreien Sprachen (KFS) beinhaltet alle Sprachen, die von einem nichtdeterministischen Kellerautomaten akzeptiert werden.
Jede dieser Sprachen wird kontextfrei genannt.
Bemerkungen
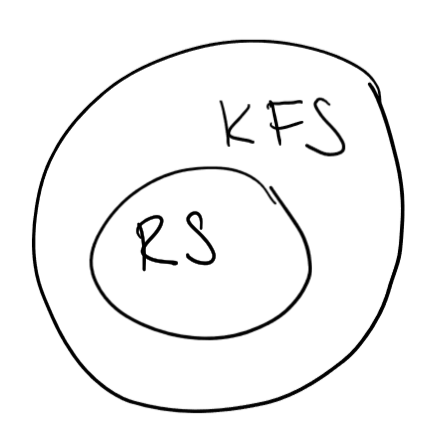
- Diese Definition ist äquivalent zur Definition von kontextfreien Sprachen, welche auf einem generierenden Mechanismus basiert.
- Die Klasse der kontextfreien Sprachen beinhaltet die Klasse der regulären Sprache (da jeder EA als NKA interpretiert werden kann).
- Es gibt weitere Klassen von Sprachen. mehr dazu
Beispiel
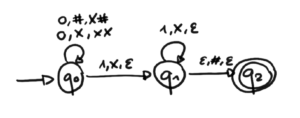
Die Sprache vom gezeichneten Kellerautomat \(M\) ist die kontextfreie Sprache \( L=\{ 0^n1^n | n \in \mathbb{N}_{ > 0} \}\).
Hier haben Sie die Option Ihre Notizen zu diesem Abschnitt hochzuladen. Wir empfehlen eine sinnvolle Beschriftung z.B. 3_2_akzept_Notizen.